
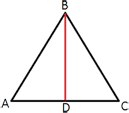
 Сторона равностороннего треугольника равна 10√
Сторона равностороннего треугольника равна 10√
По
определению равностороннего треугольника:
AB=BC=AC=10√
По
свойству равностороннего треугольника,
биссектриса является так же и
медианой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2.
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
(10√
100*3=BD2+(5√
300=BD2+25*3
300=BD2+75
BD2=225
BD=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
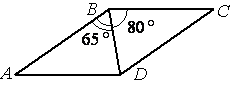 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Стороны AC, AB, BC треугольника ABC равны 2√
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.
 Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Комментарии:
(2017-03-30 23:06:34) Администратор: Акиф, в решении есть ссылки на материалы, на которые я ссылаюсь в решении - это первое. Поясните, начиная с какой строки Вам непонятно...Я обязательно поясню.
(2017-03-29 22:54:04) Акиф: Можете по подробней объяснить ?