
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ763 –Η–Ζ 1087 |
 –ö –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è AB –Η ―¹–Β–Κ―É―â–Α―è AO. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Β―¹–Μ–Η AB=21, AO=75.
–ö –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è AB –Η ―¹–Β–Κ―É―â–Α―è AO. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Β―¹–Μ–Η AB=21, AO=75.
 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–£.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–£.
–û―²―Ä–Β–Ζ–Ψ–Κ OB - ―ç―²–Ψ ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η ―ç―²–Ψ―² –Ψ―²―Ä–Β–Ζ–Ψ–Κ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ AB (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É
–Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ AOB -
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι, ―²–Ψ–≥–¥–Α, –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AO2=AB2+OB2
752=212+OB2
5625=441+OB2
OB2=5184
OB=72=R
–û―²–≤–Β―²: 72
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 100 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 230 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 320 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
–ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 100 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 230 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η (–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 320 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
–Θ–Κ–Α–Ε–Η―²–Β –Ϋ–Ψ–Φ–Β―Ä–Α –≤–Β―Ä–Ϋ―΄―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι.
1) –ï―¹–Μ–Η –¥–≤–Α ―É–≥–Μ–Α –Ψ–¥–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ –¥–≤―É–Φ ―É–≥–Μ–Α–Φ –¥―Ä―É–≥–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―²–Ψ ―²–Α–Κ–Η–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η –Ω–Ψ–¥–Ψ–±–Ϋ―΄.
2) –£–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ―΄–Β ―É–≥–Μ―΄ ―Ä–Α–≤–Ϋ―΄.
3) –¦―é–±–Α―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―è–≤–Μ―è–Β―²―¹―è –Β–≥–Ψ –Φ–Β–¥–Η–Α–Ϋ–Ψ–Ι.
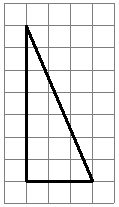 –ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1Ο½1 –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Β–≥–Ψ –±–Ψ–Μ―¨―à–Β–≥–Ψ –Κ–Α―²–Β―²–Α.
–ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β ―¹ ―Ä–Α–Ζ–Φ–Β―Ä–Ψ–Φ –Κ–Μ–Β―²–Κ–Η 1Ο½1 –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –Β–≥–Ψ –±–Ψ–Μ―¨―à–Β–≥–Ψ –Κ–Α―²–Β―²–Α.
–Ξ–Ψ–Ζ―è–Η–Ϋ ―É―΅–Α―¹―²–Κ–Α –Ω–Μ–Α–Ϋ–Η―Ä―É–Β―² ―É―¹―²―Ä–Ψ–Η―²―¨ –≤ –Ε–Η–Μ–Ψ–Φ –¥–Ψ–Φ–Β –Ζ–Η–Φ–Ϋ–Β–Β –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η–Β. –û–Ϋ ―Ä–Α―¹―¹–Φ–Α―²―Ä–Η–≤–Α–Β―² –¥–≤–Α –≤–Α―Ä–Η–Α–Ϋ―²–Α: ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–Β –Η–Μ–Η –≥–Α–Ζ–Ψ–≤–Ψ–Β –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η–Β. –Π–Β–Ϋ―΄ –Ϋ–Α –Ψ–±–Ψ―Ä―É–¥–Ψ–≤–Α–Ϋ–Η–Β –Η ―¹―²–Ψ–Η–Φ–Ψ―¹―²―¨ –Β–≥–Ψ ―É―¹―²–Α–Ϋ–Ψ–≤–Κ–Η, –¥–Α–Ϋ–Ϋ―΄–Β –Ψ ―Ä–Α―¹―Ö–Ψ–¥–Β –≥–Α–Ζ–Α, ―ç–Μ–Β–Κ―²―Ä–Ψ―ç–Ϋ–Β―Ä–≥–Η–Η –Η –Η―Ö ―¹―²–Ψ–Η–Φ–Ψ―¹―²–Η –¥–Α–Ϋ―΄ –≤ ―²–Α–±–Μ–Η―Ü–Β.
| –ù–Α–≥―Ä–Β–≤–Α―²–Β–Μ―¨ (–Κ–Ψ―²―ë–Μ) | –ü―Ä–Ψ―΅–Β–Β –Ψ–±–Ψ―Ä―É–¥–Ψ–≤–Α–Ϋ–Η–Β –Η –Φ–Ψ–Ϋ―²–Α–Ε | –Γ―Ä–Β–¥–Ϋ. ―Ä–Α―¹―Ö–Ψ–¥ –≥–Α–Ζ–Α/ ―¹―Ä–Β–¥–Ϋ. –Ω–Ψ―²―Ä–Β–±–Μ. –Φ–Ψ―â–Ϋ–Ψ―¹―²―¨ | –Γ―²–Ψ–Η–Φ–Ψ―¹―²―¨ –≥–Α–Ζ–Α/―ç–Μ–Β–Κ―²―Ä–Ψ¬≠―ç–Ϋ–Β―Ä–≥–Η–Η | |
| –™–Α–Ζ–Ψ–≤–Ψ–Β –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η–Β | 24 000 ―Ä―É–±. | 18 280 ―Ä―É–±. | 1,2 –Κ―É–±. –Φ/―΅ | 5,6 ―Ä―É–±./–Κ―É–±. –Φ |
| –≠–Μ–Β–Κ―²―Ä. –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η–Β | 20 000 ―Ä―É–±. | 15 000 ―Ä―É–±. | 5,6 –Κ–£―² | 3,8 ―Ä―É–±./(–Κ–£―²*―΅) |
–û–±–¥―É–Φ–Α–≤ –Ψ–±–Α –≤–Α―Ä–Η–Α–Ϋ―²–Α, ―Ö–Ψ–Ζ―è–Η–Ϋ ―Ä–Β―à–Η–Μ ―É―¹―²–Α–Ϋ–Ψ–≤–Η―²―¨ –≥–Α–Ζ–Ψ–≤–Ψ–Β –Ψ–±–Ψ―Ä―É–¥–Ψ–≤–Α–Ϋ–Η–Β. –ß–Β―Ä–Β–Ζ ―¹–Κ–Ψ–Μ―¨–Κ–Ψ ―΅–Α―¹–Ψ–≤ –Ϋ–Β–Ω―Ä–Β―Ä―΄–≤–Ϋ–Ψ–Ι ―Ä–Α–±–Ψ―²―΄ –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η―è ―ç–Κ–Ψ–Ϋ–Ψ–Φ–Η―è –Ψ―² –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ–Η―è –≥–Α–Ζ–Α –≤–Φ–Β―¹―²–Ψ ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹―²–≤–Α –Κ–Ψ–Φ–Ω–Β–Ϋ―¹–Η―Ä―É–Β―² ―Ä–Α–Ζ–Ϋ–Ψ―¹―²―¨ –≤ ―¹―²–Ψ–Η–Φ–Ψ―¹―²–Η ―É―¹―²―Ä–Ψ–Ι―¹―²–≤–Α –≥–Α–Ζ–Ψ–≤–Ψ–≥–Ψ –Η ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–≥–Ψ –Ψ―²–Ψ–Ω–Μ–Β–Ϋ–Η―è?
 –£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OCD ―Ä–Α–≤–Β–Ϋ 55¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OAB.
–£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OCD ―Ä–Α–≤–Β–Ϋ 55¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OAB.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2023-02-14 01:23:05) : –ß–Β―Ä–Β–Ζ –Κ–Ψ–Ϋ―Ü―΄ –ê, –£ ―Ö–Ψ―Ä–¥―΄ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –ê–Γ –Η –£–Γ. –Θ–≥–Ψ–Μ –ê–Γ–£ ―Ä–Α–≤–Β–Ϋ 130¬Α. –ù–Α–Ι–¥–Η―²–Β –≥―Ä–Α–¥―É―¹–Ϋ―É―é –≤–Β–Μ–Η―΅–Η–Ϋ―É –Φ–Β–Ϋ―¨―à–Β–Ι –¥―É–≥–Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Κ–Ψ―²–Ψ―Ä–Α―è ―¹―²―è–≥–Η–≤–Α–Β―²―¹―è ―Ö–Ψ―Ä–¥–Ψ–Ι –ê–£. –£ –Ψ―²–≤–Β―² –Ζ–Α–Ω–Η―à–Η―²–Β ―²–Ψ–Μ―¨–Κ–Ψ ―΅–Η―¹–Μ–Ψ.