
 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Площадь
трапеции вычисляется по формуле  , где a и b - основания трапеции, а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
, где a и b - основания трапеции, а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
 Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине гипотенузы (
по свойству прямоугольного треугольника), h=3/2=1,5. Используя формулу площади трапеции получаем S=(2+6)*1,5/2. Вычисляем S=6.
Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине гипотенузы (
по свойству прямоугольного треугольника), h=3/2=1,5. Используя формулу площади трапеции получаем S=(2+6)*1,5/2. Вычисляем S=6.
Ответ: S=6.
Поделитесь решением
Присоединяйтесь к нам...
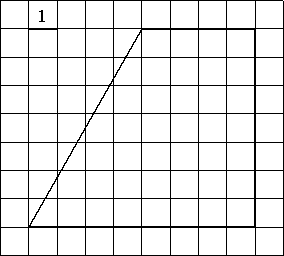 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
 Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
 Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Комментарии:
(2016-02-06 21:50:52) Дарья: Спасибо огромное автору и сайту за проделанную работу.Это очень помогает и выручает в той ситуации,когда не можешь решить то или иное задание.Спасибо!