
Известно, что графики функций y=x2+p и y=2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Чтобы найти общую точку двух графиков, надо найти решение системы, составленное из уравнений этих графиков:
 y=x2+p
y=x2+p
y=2x-2
x2+p=2x-2
x2-2x+p+2=0
Это квадратное уравнение должно иметь только один корень, т.к. по условию, графики пересекаются только в одной точке. Следовательно, дискриминант должен быть равен нулю.
D=(-2)2-4*1*(p+2)=4-4p-8=-4-4p=0
p=-1
Получаем уравнение:
x2-2x-1+2=0
x2-2x+1=0
(x-1)2=0
x=1 - это координата х точки пересечения.
y=2x-2=2*1-2=0 - это координата y точки пересечения.
Получаем: координаты точки пересечения графиков (1;0).
 Построим графики по точкам:
Построим графики по точкам:
y=x2+p=x2-1 (Красный график)
| X | -2 | -1 | 0 | 1 | 2 |
| Y | 3 | 0 | -1 | 0 | 3 |
| X | 0 | 1 | 2 |
| Y | -2 | 0 | 2 |
Поделитесь решением
Присоединяйтесь к нам...
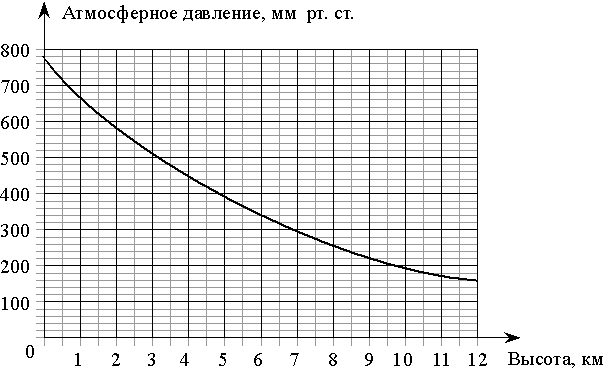 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 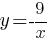 Б)
Б) 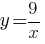 В)
В) 
ГРАФИКИ
1) 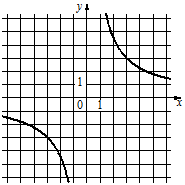 2)
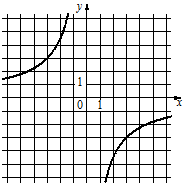
2) 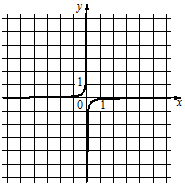 3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c>0 2) a<0, c<0 3) a>0, c<0 4) a>0, c>0 |
А)  |
Б)  |
В)  |
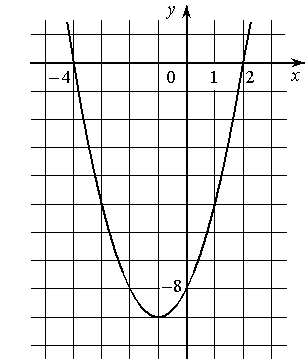 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Наименьшее значение функции равно -8
2) f(-4)>f(1)
3) f(x)<0 при -4<x<2
Постройте график функции y=4|x-3|-x2+8x-15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Комментарии: