Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
Рассмотрим каждое утверждение.
1) "Вокруг любого треугольника можно описать окружность", это утверждение верно (по
теореме об окружности)
2) "Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны". Это утверждение верно (по
свойству углов).
3) "Площадь треугольника не превышает произведения двух его сторон." Площадь треугольник можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
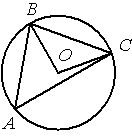Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
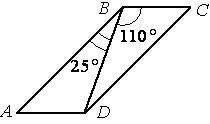Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: