
На координатной прямой отмечены числа a и b.
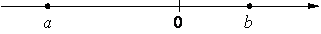
Какое из приведённых утверждений неверно?
1) ab2>0
2) b-a>0
3) ab<0
4) a+b<0
Внимательно посмотрев на картинку, можно увидеть, что b - положительное число и стоит ближе к нулю, чем а (отрицательное число). Т.е. |b|<|a|, тогда:
1) ab2>0, b2 - положительное число (квадрат любого числа всегда положителен), и это положительное число умножено на отрицательное, результат будет отрицательным (так как плюс на минус дает минус). Следовательно, это утверждение неверно.
2) b-a>0, положительное число минус отрицательное число, тоже самое, что положительное плюс положительное. Результат, естественно, будет положительным. Например: 2-(-5)=2+5=7 Таким образом, это утверждение верно
3) ab<0, отрицательное число умноженное на положительное дает число отрицательное (минус на плюс дает минус). Таким образом, это утверждение верно
4) a+b<0, простыми словами объяснить можно так: большое отрицательное число + небольшое положительное, тоже самое, что и небольшое положительное число минус большое положительное. Разница будет меньше нуля. Например: -10+5=5-10=-5. Таким образом, это утверждение верно
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 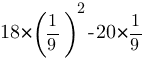
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 99 человек. Голоса между кандидатами распределились в отношении 2:9. Сколько голосов получил победитель?
Найдите значение выражения (2,9*10-5)(2*10-2).
1) 0,0000058
2) 0,000000058
3) 58000000000
4) 0,00000058
Найдите значение выражения 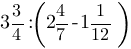
На координатной прямой отмечены точки A, B, C, и D.
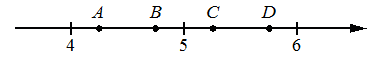
Одна из них соответствует числу 100/21. Какая это точка?
1) точка A
2) точка B
3) точка C
4) точка D
Комментарии: