
Стороны AC, AB, BC треугольника ABC равны 3√
 По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 3√
По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 3√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. /KAC=/ABC. /ACK не равен /ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому /ACK = /BAC. Следовательно, /AKC=/ACB => cos(/AKC)=cos(/ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(/ACB).
(√
14=9*2+1-6*√
14-19=-6*√
5=6*√
cos(/AKC)=cos(/ACB)=5/(6*√
Ответ: cos(/AKC)=5/(6*√
Поделитесь решением
Присоединяйтесь к нам...
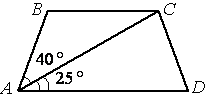 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
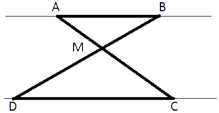 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
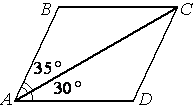 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
 Площадь прямоугольного треугольника равна 800√
Площадь прямоугольного треугольника равна 800√
Комментарии:
(2017-03-30 23:04:20) Администратор: БМБ, решите свою задачу по аналогии с этой.
(2017-03-29 22:10:44) БМБ: Стороны AC, AB, BCтреугольника ABC равны и 2 коня из 3 и корень из 7 1 соответственно. Точка K расположе‐ на вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K , A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90° .
(2017-03-29 22:03:07) БМБ: . Стороны AC, AB, BC треугольника ABC равны ,3корня из 2 ,корень из 14 и 1 соответственно. Точка K расположе‐ на вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90°