
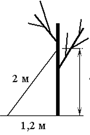
 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестница, дерево и земля представляют из себя прямоугольный треугольник. Высоту, на которой находится конец лестницы обозначим как х.
Тогда по теореме Пифагора мы можем записать 22=1,22+x2. Отсюда, x2=4-1,44, х2=2,56, x=1,6.
Ответ: 1,6 метра.
Поделитесь решением
Присоединяйтесь к нам...
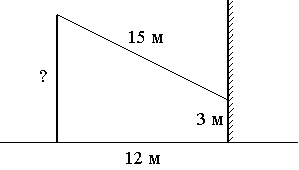 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
 В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
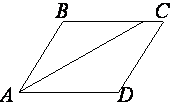 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
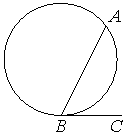 На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Комментарии:
(2016-10-18 14:04:11) Администратор: катя, поясните, что значит не та задача?
(2016-10-17 11:54:51) катя: это не та задача как её решить
(2016-05-13 12:32:54) Ульяна: спасибо, очень хорошо объяснили
(2015-12-06 12:47:55) Солнышко: Это задача, очень важная!!! Спасибо)))
(2015-05-26 21:59:28) ангел: спасибо)
(2015-03-19 20:03:56) Администратор: Ишак, корень квадратный из 2,56 это 1,6.
(2015-03-19 19:54:20) Ишак: Откуда 1,6 ?