Из двух городов одновременно навстречу друг другу отправляются два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 56 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 182 км, скорость первого велосипедиста равна 13 км/ч, скорость второго — 15 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Обозначим:
S1 - путь, который проехал первый велосипедист.
S2 - путь, который проехал второй велосипедист.
t1 - время в пути первого велосипедиста.
t2 - время в пути второго велосипедиста.
S1+S2=182 км.
Первый велосипедист ехал на 56 минут меньше второго, т.к. сделал остановку.
56 минут = 56/60 часа.
t2=t1+56/60 минут
Получается:
S1=13*t1
S2=15*t2
13*t1+15*t2=182
13t1+15(t1+56/60)=182
13t1+15t1+15*56/60=182
28t1=182-56/4
28t1=168
t1=6
S1=13*t1=13*6=78
S1+S2=182
S2=182-S1=182-78=104
Ответ: S2=104 км
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений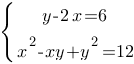 
Решите уравнение x(x2+2x+1)=6(x+1)
Решите систему уравнений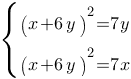 
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=-2x имеет с графиком ровно одну общую точку.
Из пунктов А и В, расстояние между которыми 19 км, одновременно навстречу друг другу вышли два туриста и встретились в 10 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 1 км/ч меньшей, чем турист, шедший из А.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-03-01 11:14:44) Администратор: WWE_R0mEn_12345_2018, в одном часе 60 минут, т.е. час разбит на 60 частей. Мы берем 56 минут (т.е. таких частей), т.е. мы взяли 56 от 60, иначе 56/60 часа.
(2019-02-26 18:00:46) WWE_R0mEn_12345_2018: 56=почему 56/60 часа