
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ18 –Є–Ј 1087 |
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –і–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤ —З–µ—В—Л—А–µ —А–∞–Ј–∞ –±–Њ–ї—М—И–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ AKD.
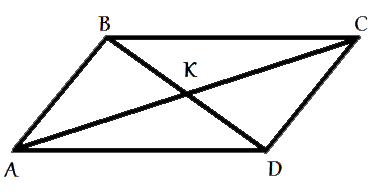 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC –Є ACD.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC –Є ACD.
–°—В–Њ—А–Њ–љ–∞ AC - –Њ–±—Й–∞—П –і–ї—П —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤.
AB=CD –Є BC=AD (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є —А–∞–≤–љ—Л (–њ–Њ
—В—А–µ—В—М–µ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г). –Р –Ј–љ–∞—З–Є—В —А–∞–≤–љ—Л –Є –Є—Е –њ–ї–Њ—Й–∞–і–Є, –Є —А–∞–≤–љ—Л —Н—В–Є –њ–ї–Њ—Й–∞–і–Є –њ–Њ–ї–Њ–≤–Є–љ–µ –њ–ї–Њ—Й–∞–і–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ACD.
–Ъ–∞–Ї —В–Њ–ї—М–Ї–Њ —З—В–Њ –≤—Л—П—Б–љ–Є–ї–Є, –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ–ї–Њ—Й–∞–і–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ю—В—А–µ–Ј–Њ–Ї DK - —П–≤–ї—П–µ—В—Б—П
–Љ–µ–і–Є–∞–љ–Њ–є (–њ–Њ —В—А–µ—В—М–µ–Љ—Г
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞), –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –і–µ–ї–Є—В —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ –і–≤–∞ —А–∞–≤–љ–Њ–≤–µ–ї–Є–Ї–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В.–µ. —А–∞–≤–љ—Л—Е –њ–Њ –њ–ї–Њ—Й–∞–і–Є (
—Б–≤–Њ–є—Б—В–≤–Њ –Љ–µ–і–Є–∞–љ—Л).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –њ–ї–Њ—Й–∞–і—М AKD —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ACD.
SAKD=SACD/2=SABCD/4.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=5, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 5.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=5, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 5.
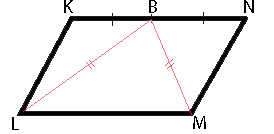 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ KLMN —В–Њ—З–Ї–∞ B вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л KN. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ BL=BM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ KLMN —В–Њ—З–Ї–∞ B вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л KN. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ BL=BM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 36, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 36, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 38, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 38, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 8.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 8.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2019-05-10 12:02:43) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь–∞—И–∞, DK - –Љ–µ–і–Є–∞–љ–∞ –њ–Њ —В—А–µ—В—М–µ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –Ї–Њ—В–Њ—А–Њ–µ –≥–ї–∞—Б–Є—В, —З—В–Њ –і–Є–∞–≥–Њ–љ–∞–ї–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –Є —В–Њ—З–Ї–Њ–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–µ–ї—П—В—Б—П –њ–Њ–њ–Њ–ї–∞–Љ. –Т —А–µ—И–µ–љ–Є–Є –µ—Б—В—М —Б—Б—Л–ї–Ї–Є –љ–∞ —Н—В–Є –Љ–∞—В–µ—А–Є–∞–ї—Л, –љ–∞–ґ–Є–Љ–∞–є—В–µ –љ–∞ –љ–Є—Е.
(2019-05-10 09:50:42) –Ь–∞—И–∞: –Я–Њ—З–µ–Љ—Г –Ф–Ъ —П–≤–ї—П–µ—В—Б—П –Љ–µ–і–Є–∞–љ–Њ–є –Є –і–µ–ї–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ 2 —А–∞–≤–љ–Њ–≤–µ–ї–Є–Ї–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞,–љ–µ –Њ—З–µ–љ—М –њ–Њ–љ—П—В–љ–Њ?
(2016-01-17 15:35:44) –Ь–∞—А–≥–∞—А–Є—В–∞: –°–њ–∞—Б–Є–±–Њ –Њ–≥—А–Њ–Љ–љ–Њ–µ! –Ю—З–µ–љ—М –њ–Њ–Љ–Њ–≥–ї–Њ)
(2015-05-24 18:28:57) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–љ—В–Њ—И, —Н—В–Њ —Б–≤–Њ–є—Б—В–≤–Њ –Љ–µ–і–Є–∞–љ—Л.
(2015-05-24 18:12:51) –Р–љ—В–Њ—И: –Р –њ–Њ—З–µ–Љ—Г –Љ–µ–і–Є–∞–љ–∞ –і–µ–ї–Є—В –љ–∞ –і–≤–∞ —А–∞–≤–љ–Њ–≤–µ–ї–Є–Ї–Є—Е?
(2015-01-08 12:21:10) : cgfcb,j