
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
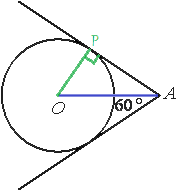 Проведем отрезок АО, данный отрезок равен 8 (по условию задачи).
Проведем отрезок АО, данный отрезок равен 8 (по условию задачи).
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР.
АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Соответственно угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin∠30°=1/2 (табличное значение).
sin∠PAO=ОР/АО (по определению синуса).
Получается:
ОР/АО=1/2
OP=AO/2=8/2=4 - это и есть радиус окружности.
Ответ: R=4.
Поделитесь решением
Присоединяйтесь к нам...
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Площадь прямоугольного треугольника равна 392√
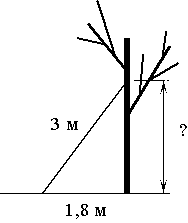 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
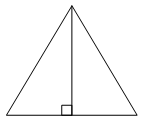 Высота равностороннего треугольника равна 78√
Высота равностороннего треугольника равна 78√
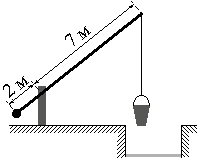 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии: