
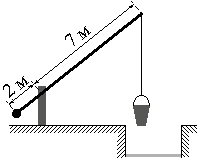 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
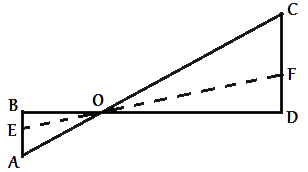 Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
1) /BOA=/DOC, т.к. они
вертикальные.
2) /OBA=/ODC=90°
3) /BAO=/DCO, т.к. они
внутренние накрест-лежащие.
Следовательно, треугольники ABO и COD
подобны (по признаку подобия). Отсюда следует, что CO/AO=CD/AB. Поэтому при движении, высота концов журавля будет подчиняться этой же пропорции.
CO/AO=CD/AB=CF/AE
7/2=CF/1 => CF=7/2=3,5.
Ответ: конец длинного плеча опустится на 3,5 метра.
Поделитесь решением
Присоединяйтесь к нам...
 Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
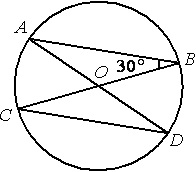 В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
 Площадь прямоугольного треугольника равна 32√
Площадь прямоугольного треугольника равна 32√
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Комментарии:
(2017-02-01 15:17:22) Администратор: Ксения, все решение перед Вами, нажимайте на ссылки в решении, будут показаны материалы, на которые я ссылаюсь при решении.
(2017-01-29 16:54:43) Ксения: А по какой формуле или правилу решается эта задача?
(2017-01-14 20:09:42) Администратор: Яна, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-12 17:03:53) Яна: 1 2,5 Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большей опоры. Ответ дайте в метрах.