Решите неравенство (2x-5)2≥(5x-2)2.
(2x-5)2≥(5x-2)2
(2x-5)2-(5x-2)2≥0
Воспользуемся формулой
разность квадратов:
((2x-5)-(5x-2))((2x-5)+(5x-2))≥0
(2x-5-5x+2)(2x-5+5x-2)≥0
(-3x-3)(7x-7)≥0
(-3)(x+1)(7x-7)≥0 |:(-3)
(x+1)(7x-7)≤0
Заметим, что знак поменялся на противоположный, так как мы разделили левую и правую части на отрицательное число.
7(x+1)(x-1)≤0 |:7
(x+1)(x-1)≤0
x2-1≤0
Это квадратичная функция, так как коэффициент "а"=1, т.е. больше нуля, то ветви параболы направлены вверх. Корни уравнения x2-1=0 это x1=-1, x2=1
Данная функция меньше или равна нулю, когда график лежит ниже оси Х, т.е. в диапазоне между корнями:
x⊂[-1;1]
Ответ: x⊂[-1;1]
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства
2x-x2≤0
1) (-∞;0]∪[2;+∞)
2) [0;+∞)
3) [2;+∞)
4) [0;2]
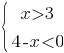
Укажите решение системы неравенств
1) 
2) 
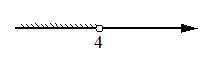
3) 
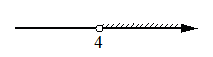
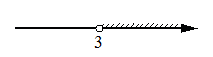
4) 
О числах a и c известно, что a<c. Какое из следующих неравенств неверно
1) a-29<c-29
2) -a/5<-c/5
3) a+32<c+32
4) -a/17<c/17
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: