
В геометрической прогрессии сумма первого и второго членов равна 200, а сумма второго и третьего членов равна 50. Найдите первые три члена этой прогрессии.
Каждый член
геометрической прогрессии можно выразить через первый член.
bn=b1qn-1
Тогда b2=b1q2-1=b1q
По условию:
1) b1+b2=200
b1+b1q=200
b1(1+q)=200
2) b2+b3=50
b1q+b1q2=50
b1(q+q2)=50
b1(q+1)q=50
Подставляем из п. 1)
200q=50 => q=0,25, тогда b1(1+0,25)=200 => b1=160
b2=160*0,25=40
b3=160*0,252=10
Ответ: b1=160, b2=40, b3=10
Поделитесь решением
Присоединяйтесь к нам...
Выписаны первые несколько членов арифметической прогрессии: -7; -5; -3; … Найдите её шестнадцатый член.
В первом ряду кинозала 25 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в шестом ряду?
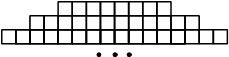 Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадрата больше, чем в предыдущей. Сколько квадратов в 54-й строке?
Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадрата больше, чем в предыдущей. Сколько квадратов в 54-й строке?
Геометрическая прогрессия (bn) задана условиями:
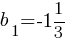 , bn+1=-3bn.
, bn+1=-3bn.
Найдите b7.
Геометрическая прогрессия (bn) задана условиями: b1=64, bn+1=bn*1/2. Найдите b7.
Комментарии: