
Задача №20 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
А) 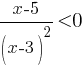
|
1) 
|
Б) 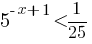
|
2) 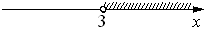
|
| В) (x-3)(x-5)>0 |
3) 
|
| Г) log2(x-3)<1 |
4) 
|
Решим каждое неравенство:
А) 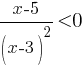
Это неравенство будет меньше нуля, только когда числитель будет меньше нуля, так как знаменатель всегда положителен. Следовательно, данное неравенство можно упростить:
x-5<0 => x<5, подходит вариант 4).
Б) 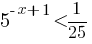
5-x+1<5-2
Применим теорему для решения показательных неравенств:
-x+1<-2 (знак сохраняется так как 5>1)
-x<-3 |*(-1)
x>3 (знак поменялся так как мы домножили на отрицательное число).
Подходит вариант 2).
В) (x-3)(x-5)>0
Найдем корни соответствующего уравнения:
(x-3)(x-5)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-3=0 => x1=3
2) x-5=0 => x2=5
x2-5x-3x+15>0
x2-8x+15>0

График данной функции - парабола, коэффициент а=1, т.е. положительный, следовательно ветви параболы направлены вверх.
Функция больше нуля, когда ее график располагается выше оси Х. В данном случае на диапазонах (-∞3) и (5;+∞) - подходит вариант 1).
Г) log2(x-3)<1
По второму свойству логарифмов преобразуем правую часть неравенства:
log2(x-3)
По теореме для решения логарифмических неравенств:
 x-3<2
x-3<2
x-3>0
 x<5
x<5
x>3
Подходит вариант 3).
Ответ:
A)
Б)
В)
Г)
4)
2)
1)
3)
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) масса футбольного мяча | 1) 18 кг |
| Б) масса дождевой капли | 2) 2,8 т |
| В) масса взрослого бегемота | 3) 20 мг |
| Г) масса стиральной машины | 4) 750 г |
Найдите корень уравнения 9x+2(1-6x)=-x-6.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) рост жирафа | 1) 6400 км |
| Б) толщина лезвия бритвы | 2) 500 см |
| В) радиус Земли | 3) 0,08 мм |
| Г) ширина футбольного поля | 4) 68 м |
Решите уравнение x2+10x+21=0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Некоторые учащиеся 11-х классов школы ходили в октябре на спектакль «Вишнёвый сад». В декабре некоторые одиннадцатиклассники пойдут
на постановку по пьесе «Три сестры», причём среди них не будет тех, кто ходил в октябре на спектакль «Вишнёвый сад».
Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из одиннадцатиклассников пойдёт на постановку по пьесе «Три сестры».
1) Нет ни одного одиннадцатиклассника, который ходил на спектакль «Вишнёвый сад» и пойдёт на постановку по пьесе «Три сестры».
2) Каждый учащийся 11-х классов, который не был на спектакле «Вишнёвый сад», пойдёт на постановку по пьесе «Три сестры».
3) Среди учащихся 11-х классов этой школы, которые не пойдут на постановку по пьесе «Три сестры», есть хотя бы один, который ходил на спектакль «Вишнёвый сад».
4) Найдётся одиннадцатиклассник, который не ходил на спектакль «Вишнёвый сад» и не пойдёт на постановку по пьесе «Три сестры».
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Комментарии: