Постройте график функции y=x2-|4x+3| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
x2-(4x+3), при 4x+3≥0
x2-(-(4x+3)), при 4x+3<0
x2-4x-3, при 4x≥-3
x2+(4x+3), при 4x<-3
x2-4x-3, при x≥-3/4
x2+4x+3, при x<-3/4
Рассмотрим и построим график для каждой подфункции и объединим их.
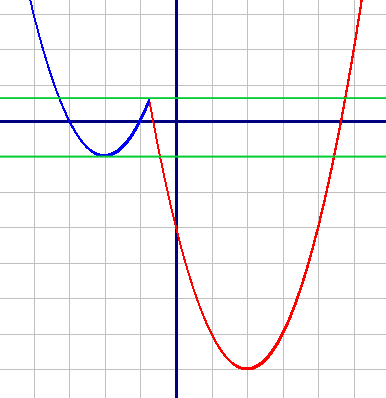1) y1=x2-4x-3, при x≥-3/4 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | -3 | -6 | -7 | -6 |
| X | -1 | -2 | -3 | -4 |
| Y | 0 | -1 | 0 | 3 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=2|x-5|-x2+11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции y=x2+11x-4|x+6|+30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Постройте график функции y=|x|x-|x|-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=|x2+5x+6| . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-17 22:32:53) Ваня: у=х^2-|2х+1|
(2021-11-04 17:37:18) : Вычислить площадь фигуры, ограниченной линиями y = x2 – 4x + 3 и y = x – 1. Построить график.
(2017-03-06 23:34:01) Администратор: Анастасия, -3/4 - это точка излома графика или можно сказать, что это граница двух подграфиков. Посмотрите на полученную систему.
(2017-03-06 16:15:20) Анастасия : А почему нужно подставлять - 3/4?