
Постройте график функции y=x2-9x-2|x-4|+20 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Так как функция содержит модуль, значит функцию надо разбить на две подфункции:
 x2-9x-2(x-4)+20, при (x-4)≥0
x2-9x-2(x-4)+20, при (x-4)≥0
x2-9x-2(-(x-4))+20, при (x-4)<0
 x2-9x-2x+8+20, при x≥4
x2-9x-2x+8+20, при x≥4
x2-9x+2(x-4)+20, при x<4
 x2-11x+28, при x≥4
x2-11x+28, при x≥4
x2-9x+2x-8+20, при x<4
 x2-11x+28, при x≥4
x2-11x+28, при x≥4
x2-7x+12, при x<4
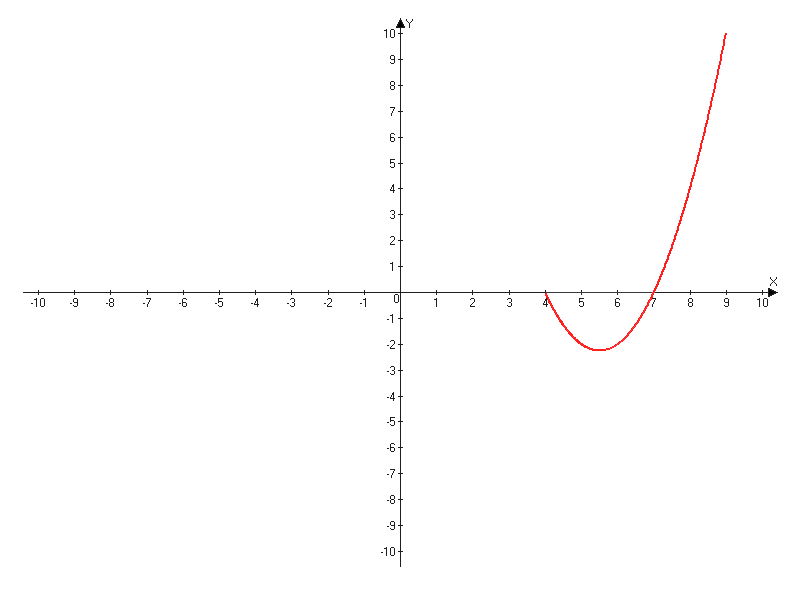
Построим график первой подфункции:
Найдем
корни уравнения x2-11x+28=0
D=(-11)2-4*1*28=121-112=9
x1=(-(-11)+3)/2=7
x2=(-(-11)-3)/2=4
| X | 4 | 5 | 6 | 7 |
| Y | 0 | -2 | -2 | 0 |
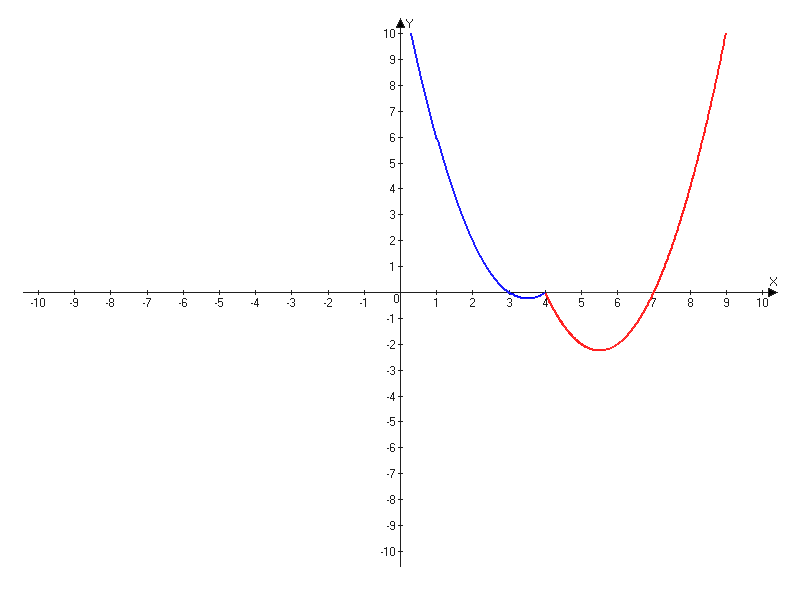
| X | 4 | 3 | 2 | 1 |
| Y | 0 | 0 | 2 | 6 |
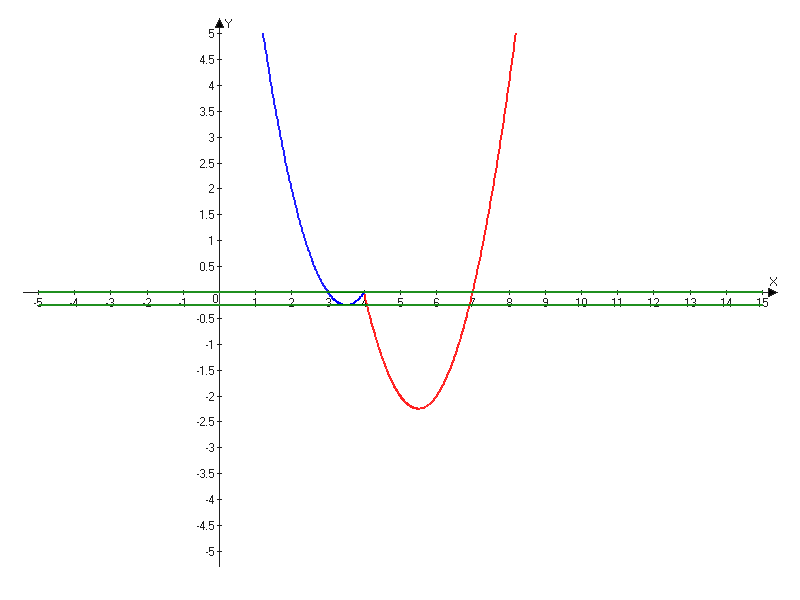
Поделитесь решением
Присоединяйтесь к нам...
Сократите дробь 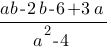
Найдите значение выражения 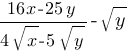 , если √
, если √
Постройте график функции y=|x|(x-1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Найдите значение выражения √
1) 28
2) 4√
3) 4
4) 16√
Значение какого из выражений является числом рациональным?
1) √
2) (√
3) √
4) √
Комментарии: