
Постройте график функции 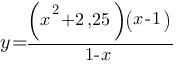 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Запишем Область Допустимых Значений (ОДЗ).
Так как на ноль делить нельзя, то 1-x≠0, т.е. x≠1
Упростим функцию:
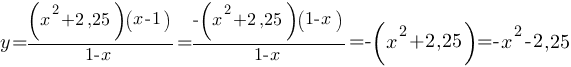
 График представляет из себя параболу. Коэффициент а=-1, т.е. меньше нуля, следовательно ветви параболы направлены вниз. Построим график по точкам:
График представляет из себя параболу. Коэффициент а=-1, т.е. меньше нуля, следовательно ветви параболы направлены вниз. Построим график по точкам:
| X | -2 | -1 | 0 | 1 |
| Y | -6,25 | -3,25 | -2,25 | -3,25 |
 y=-x2-2,25
y=-x2-2,25Поделитесь решением
Присоединяйтесь к нам...
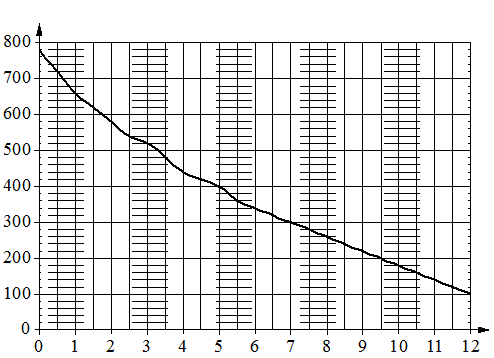 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 620 миллиметрам ртутного столба. Ответ дайте в километрах.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 620 миллиметрам ртутного столба. Ответ дайте в километрах.
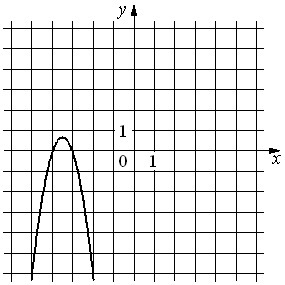 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;-2] 2) [-4;-2] 3) [-5;-4] 4) [-5;0] |
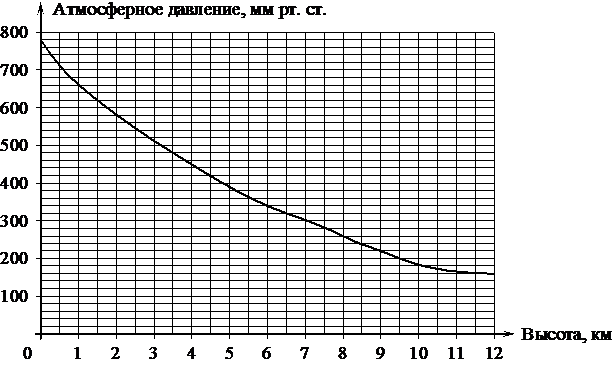 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции
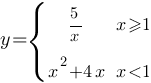 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
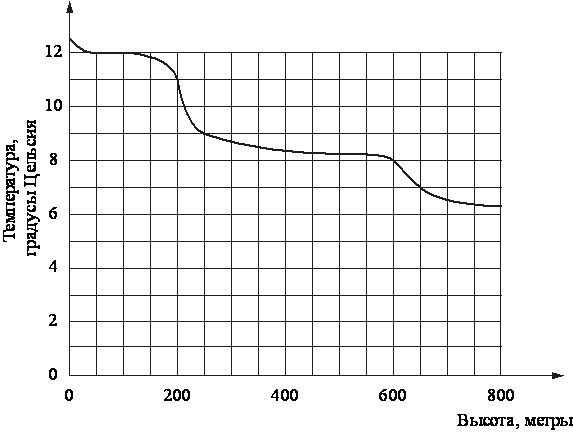 На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
Определите по графику, на сколько градусов Цельсия температура на высоте 200 метров выше, чем на высоте 650 метров.
Комментарии:
(2015-03-25 14:16:02) Администратор: Спасибо большое за найденную ошибку! Исправлено!
(2015-03-23 13:19:29) : У Вас "закралась" ошибка в нахождении третьего значения к, -3.25=к*1 к=-3.25 (выколота точка с координатами x=1)