
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ76 –Є–Ј 287 |
–Я–Њ—Б—В—А–Њ–є—В–µ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є
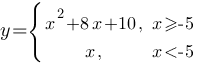
–Є –Њ–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –њ—А—П–Љ–∞—П y=m –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ —А–Њ–≤–љ–Њ –і–≤–µ –Њ–±—Й–Є–µ —В–Њ—З–Ї–Є.
–Я–Њ—Б—В—А–Њ–Є–Љ –≥—А–∞—Д–Є–Ї–Є –Њ–±–µ–Є—Е –њ–Њ–і—Д—Г–љ–Ї—Ж–Є–є –љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–Љ –Є–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–∞—Е.
–Я–µ—А–≤–∞—П –њ–Њ–і—Д—Г–љ–Ї—Ж–Є—П y=x2+8x+10, –µ—Б–ї–Є x≥-5.
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В –Є–Ј —Б–µ–±—П –њ–∞—А–∞–±–Њ–ї—Г. –Ґ–∞–Ї –Ї–∞–Ї –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В "–∞"=1 (—В.–µ. –±–Њ–ї—М—И–µ –љ—Г–ї—П), —В–Њ –≤–µ—В–≤–Є –њ–∞—А–∞–±–Њ–ї—Л –±—Г–і—Г—В –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –≤–≤–µ—А—Е.
–Т—В–Њ—А–∞—П –њ–Њ–і—Д—Г–љ–Ї—Ж–Є—П - –њ—А—П–Љ–∞—П.
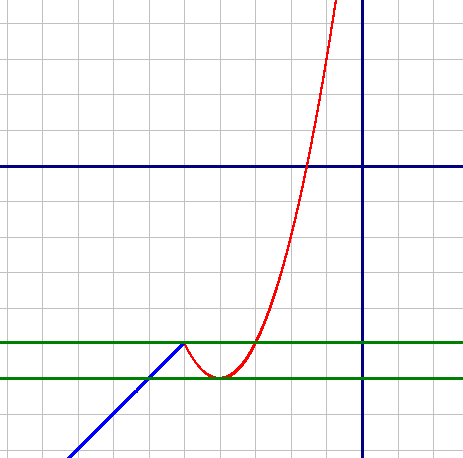 –Я–Њ—Б—В—А–Њ–Є–Љ –Њ–±–∞ –≥—А–∞—Д–Є–Ї–∞ –њ–Њ —В–Њ—З–Ї–∞–Љ:
–Я–Њ—Б—В—А–Њ–Є–Љ –Њ–±–∞ –≥—А–∞—Д–Є–Ї–∞ –њ–Њ —В–Њ—З–Ї–∞–Љ:
y=x2+8x+10, –µ—Б–ї–Є x≥-5 (–Ї—А–∞—Б–љ—Л–є).
| X | -5 | -4 | -3 | -2 |
| Y | -5 | -6 | -5 | -2 |
| X | -5 | -6 | -7 |
| Y | -5 | -6 | -7 |
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–Я–Њ—Б—В—А–Њ–є—В–µ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є
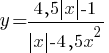
–Ю–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е k –њ—А—П–Љ–∞—П y=kx –љ–µ –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ –Њ–±—Й–Є—Е —В–Њ—З–µ–Ї.
–Я–Њ—Б—В—А–Њ–є—В–µ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є
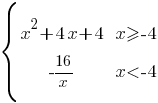
–Є –Њ–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –њ—А—П–Љ–∞—П y=m –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ –Њ–і–љ—Г –Є–ї–Є –і–≤–µ –Њ–±—Й–Є–µ —В–Њ—З–Ї–Є.
–Я–Њ—Б—В—А–Њ–є—В–µ –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є 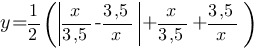 –Є –Њ–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –њ—А—П–Љ–∞—П y=m –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ —А–Њ–≤–љ–Њ –Њ–і–љ—Г –Њ–±—Й—Г—О —В–Њ—З–Ї—Г.
–Є –Њ–њ—А–µ–і–µ–ї–Є—В–µ, –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –њ—А—П–Љ–∞—П y=m –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ —А–Њ–≤–љ–Њ –Њ–і–љ—Г –Њ–±—Й—Г—О —В–Њ—З–Ї—Г.
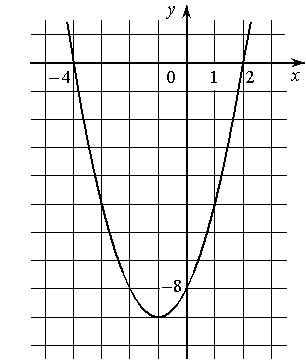 –Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –≥—А–∞—Д–Є–Ї –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є y=ƒ(x).
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –≥—А–∞—Д–Є–Ї –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є y=ƒ(x).
–Ъ–∞–Ї–Є–µ –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –Њ –і–∞–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —П–≤–ї—П—О—В—Б—П –≤–µ—А–љ—Л–Љ–Є? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –§—Г–љ–Ї—Ж–Є—П —Г–±—Л–≤–∞–µ—В –љ–∞ –њ—А–Њ–Љ–µ–ґ—Г—В–Ї–µ [-1;+∞)
2) ƒ(x)>0 –њ—А–Є x<-4 –Є –њ—А–Є x>2
3) –Э–∞–Є–Љ–µ–љ—М—И–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —А–∞–≤–љ–Њ -9
 –Э–∞ —А–Є—Б—Г–љ–Ї–µ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, –Ї–∞–Ї –Є–Ј–Љ–µ–љ—П–ї–∞—Б—М —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –≤–Њ–Ј–і—Г—Е–∞ –љ–∞ –њ—А–Њ—В—П–ґ–µ–љ–Є–Є –Њ–і–љ–Є—Е —Б—Г—В–Њ–Ї. –Я–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї–Є —Г–Ї–∞–Ј–∞–љ–Њ –≤—А–µ–Љ—П —Б—Г—В–Њ–Ї, –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–Є вАФ –Ј–љ–∞—З–µ–љ–Є–µ —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П. –Э–∞–є–і–Є—В–µ —А–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –љ–∞–Є–±–Њ–ї—М—И–Є–Љ –Є –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –њ–µ—А–≤–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ —Б—Г—В–Њ–Ї. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П.
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, –Ї–∞–Ї –Є–Ј–Љ–µ–љ—П–ї–∞—Б—М —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –≤–Њ–Ј–і—Г—Е–∞ –љ–∞ –њ—А–Њ—В—П–ґ–µ–љ–Є–Є –Њ–і–љ–Є—Е —Б—Г—В–Њ–Ї. –Я–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї–Є —Г–Ї–∞–Ј–∞–љ–Њ –≤—А–µ–Љ—П —Б—Г—В–Њ–Ї, –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–Є вАФ –Ј–љ–∞—З–µ–љ–Є–µ —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П. –Э–∞–є–і–Є—В–µ —А–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –љ–∞–Є–±–Њ–ї—М—И–Є–Љ –Є –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –≤ –њ–µ—А–≤–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ —Б—Г—В–Њ–Ї. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е –¶–µ–ї—М—Б–Є—П.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2021-10-17 20:29:25) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т–∞–ї–µ–љ—В–Є–љ–∞ –Р–ї–µ–Ї—Б–∞–љ–і—А–Њ–≤–љ–∞ –Ф–Њ–≤–≥–∞—П, –ѓ –љ–µ –њ–Њ–Љ–Њ–≥–∞—О —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –Њ—В–њ—А–∞–≤—М—В–µ –Ј–∞—П–≤–Ї—Г –љ–∞ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –Ј–∞–і–∞—З–Є, –Є —П –µ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–ї—О.
(2021-10-17 17:47:48) –Т–∞–ї–µ–љ—В–Є–љ–∞ –Р–ї–µ–Ї—Б–∞–љ–і—А–Њ–≤–љ–∞ –Ф–Њ–≤–≥–∞—П: –Ъ–∞–Ї –њ–Њ—Б—В—А–Њ–Є—В—М –≥—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є 1)—Г=2, –µ—Б–ї–Є –Љ–Њ–і—Г–ї—М —Е< –Є–ї–Є= 2; 2) —Г=-2—Е+6 –њ—А–Є —Е>2; 3) —Г=-2—Е-2, –µ—Б–ї–Є —Е<-2/ –Я—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –Ъ –њ—А—П–Љ–∞—П –Ї—Е –Є–Љ–µ–µ—В —Б –≥—А–∞—Д–Є–Ї–Њ–Љ 3 –Њ–±—Й–Є–µ —В–Њ—З–Ї–Є.