
Постройте график функции 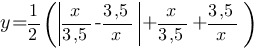 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
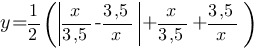
Область Допустимых Значений (ОДЗ).
x≠0 (так как делить на ноль нельзя).
Так как функция содержит
модуль, то ее надо разложить на две подфункции:
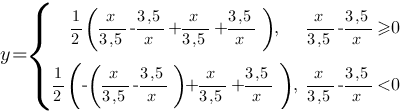
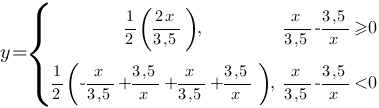


Рассмотрим каждую функцию:
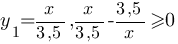
Это означает, что у=x/3,5, когда x/3,5-3,5/x≥0
Найдем этот диапазон.
x/3,5-3,5/x≥0
(x2-3,52)/(3,5x)≥0
Дробь больше нуля в двух случаях:
1) Когда и числитель и знаменатель больше нуля.
2) Когда и числитель и знаменатель меньше нуля.
Рассмотрим первый вариант:
 x2-3,52≥0
x2-3,52≥0
3,5x>0
Чтобы решить систему неравенств нужно решить каждое неравенство по отдельности и пересечь полученные диапазоны.
 x2-3,52≥0
x2-3,52≥0
x>0
Диапазон второго неравенства (0;+∞), а диапазон для первого неравенства найдем, решив уравнение x2-3,52=0
 (x-3,5)(x+3,5)=0
(x-3,5)(x+3,5)=0
x1=3,5
x2=-3,5
Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
(-∞;-3,5]∪[3,5;+∞).
Пересекаем с диапазоном второго неравенства:
(-∞;-3,5]∪[3,5;+∞)∩(0;+∞)=[3,5;+∞)
Рассмотрим второй случай, когда и числитель и знаменатель меньше нуля.
 x2-3,52<0
x2-3,52<0
3,5x<0
 x2-3,52<0
x2-3,52<0
x<0
Эту систему решать не будем, а возьмем "обратные" диапазоны, т.е. для первого неравенства диапазон будет (-3,5;3,5), а для второго (-∞;0).
Пересекаем диапазоны:
(-3,5;3,5)∩(-∞;0)=(-3,5;0)
В итоге мы получили, что:
x/3,5-3,5/x≥0 на диапазонах (-3,5;0) и [3,5;+∞)
Следовательно:
x/3,5-3,5/x<0 на диапазонах (-∞;-3,5) и (0;3,5).
Построим график функции 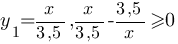 :
:
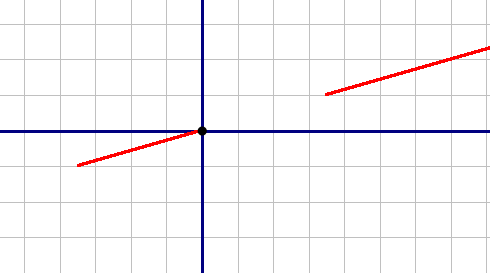 Выкалываем точку x=0 (из ОДЗ)
Выкалываем точку x=0 (из ОДЗ)
Вторая функция:
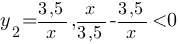
Построим график второй функции:
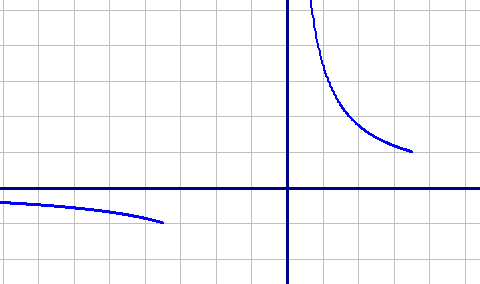
Объединяем графики:
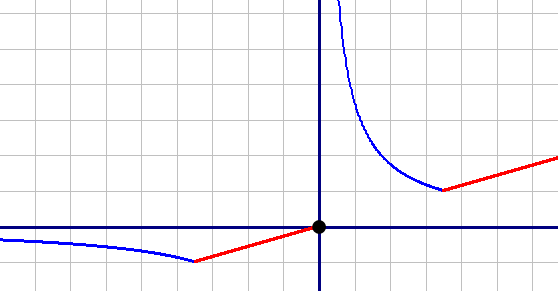
Только одна общая точки будет в двух случаях, в точках "перелома" графика, они отмечены на рисунке. Это точки -3,5 и 3,5.
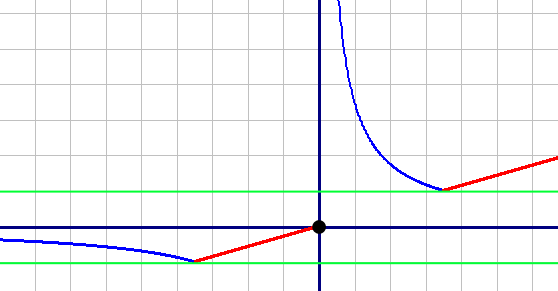
Подставим эти точки в функцию и получим значения m.
m1=y(-3,5)=-1
m2=y(3,5)=1
Ответ: m1=-1 и m2=1
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=ax2+c. Установите соответствие между графиками и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
1) a>0, c<0 2) a<0, c>0 3) a>0, c>0 4) a<0, c<0 |
А)  |
Б) 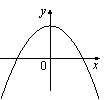 |
В) 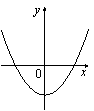 |
Г) 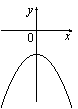 |
Постройте график функции
y=x|x|-|x|-2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=4x имеет с графиком ровно одну общую точку.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k>0, b<0 Б) k>0, b>0 В) k<0, b>0 |
1)  |
2)  |
3)  |
Постройте график функции y=x2-4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Комментарии: