Дана арифметическая прогрессия (an), для которой a6=-7,8, a19=-10,4. Найдите разность прогрессии.
Любой член
арифметической прогрессии можно записать через первый член прогрессии (a1) и разность прогрессии:
an=a1+(n-1)d
a6=a1+(6-1)d
-7,8=a1+5d
-7,8-5d=a1
a19=a1+(19-1)d
-10,4=a1+18d
-10,4=-7,8-5d+18d
-10,4+7,8=13d
-2,6=13d
d=-0,2
Ответ: -0,2
Поделитесь решением
Присоединяйтесь к нам...
Выписаны первые несколько членов арифметической прогрессии: -6; -2; 2; … Найдите её шестнадцатый член.
Последовательность задана условиями c1=-1, cn+1=cn-1. Найдите c7.
Последовательность (bn) задана условиями:
b1=-6,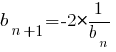 
.
Найдите b5.
Последовательность (bn) задана условиями:
b1=7, bn+1=-3*(1/bn)
Найдите b3.
Геометрическая прогрессия задана условием bn=51,5(-2)n. Найдите b4.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-10-16 22:06:00) Администратор: Иван, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-16 15:09:02) иван: 8\х-9\2хпри х1.4