
При каких положительных значениях k прямая y=kx-4 имеет с параболой y=x2-2x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Чтобы найти общую точку двух графиков, надо найти решение системы, составленное из уравнений этих графиков:
 y=kx-4
y=kx-4
y=x2-2x
kx-4=x2-2x
0=x2-2x-kx+4
0=x2-x(2+k)+4
Это квадратное уравнение должно иметь только один корень, т.к. по условию, графики пересекаются только в одной точке. Следовательно,
дискриминант должен быть равен нулю.
D=(-(2+k))2-4*1*4=(2+k)2-16=0
Раскроем скобку, используя формулу квадрат суммы:
22+2*2*k+k2-16=0
k2+4k-12=0
Это тоже квадратное уравнение, и его тоже будем решать через дискриминант:
D=42-4*1*(-12)=16+48=64
k1=(-4+8)/(2*1)=4/2=2
k2=(-4-8)/(2*1)=-12/2=-6
Напомню, что мы нашли такие k, при которых графики изначальных функций имеют только одну одну общуу точку.
По условию задачи нас интересуют только положительные k, т.е. k=2.
Подставляем это значение k в решение первоначально системы уравнений (мы остановились на моменте 0=x2-x(2+k)+4).
0=x2-x(2+2)+4
0=x2-4x+4
0=x2-4x+22
Для быстроты решения применим формулу квадрат разности:
0=(x-2)2
x=2 - это координата х точки пересечения.
Чтобы найти координату y, надо подставить это значение x и полученное значение k в любое из уравнений. Проще подставить в уравнение прямой:
y=kx-4=2*2-4=0 - это координата "y" точки пересечения.
Получаем: координаты точки пересечения графиков (2;0).
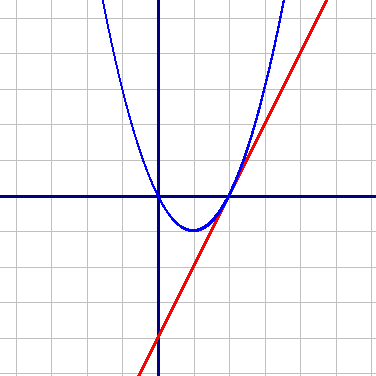 Построим графики по точкам:
Построим графики по точкам:
y=kx-4=2x-4 (Красный график)
| X | 1 | 2 | 3 |
| Y | -2 | 0 | 2 |
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -1 | 0 | 3 |
Поделитесь решением
Присоединяйтесь к нам...
При каких отрицательных значениях k прямая y=kx-4 имеет с параболой y=x2+2x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Решите систему неравенств 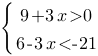
На каком рисунке изображено множество её решений?
1) 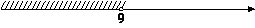
2) 
3) 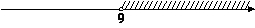
4) 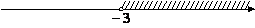
На координатной прямой отмечено число a.

Найдите наименьшее из чисел a2, a3, a4.
Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?

1) 10/23
2) 12/23
3) 13/23
4) 14/23
На координатной прямой отмечено число a.

Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-7)2<1
3) a2<36
4) a2>49
Комментарии: