
На координатной прямой отмечено число a.

Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-7)2<1
3) a2<36
4) a2>49
По координатной прямой видно, что:
6<a<7
Вычтем 6 из каждого члена неравенства:
6-6<a-6<7-6
0<a-6<1
02<(a-6)2<12
0<(a-6)2<1
Т.е. утверждение 1) неверно
Вернемся к первоначальному неравенству:
6<a<7
Вычтем 7 из каждого члена неравенства:
6-7<a-7<7-7
-1<a-7<0
возведем в квадрат, но учтем, что так как все числа отрицательные, то при возведении в квадрат знак неравенства поменяется на противоположный:
(-1)2>(a-7)2>02
1>(a-7)2>0
Т.е. утверждение 2) верно
Вернемся к первоначальному неравенству:
6<a<7
Возведем в квадрат:
62<a2<72
36<a2<49
Т.е. утверждения 3) и 4) неверны
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.
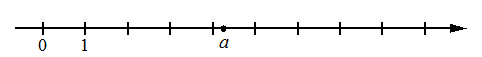
Какое из утверждений для этого числа является верным?
1) 4-a>0
2) 4-a<0
3) a-3<0
4) a-6>0
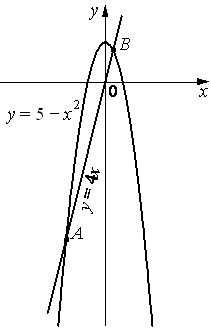 На рисунке изображены графики функций y=5-x2 и y=4x. Вычислите абсциссу точки B.
На рисунке изображены графики функций y=5-x2 и y=4x. Вычислите абсциссу точки B.
Решение какого из данных неравенств изображено на рисунке?

1) x2-36≤0
2) x2+36≤0
3) x2-36≥0
4) x2+36≥0
На координатной прямой отмечены числа x и y.
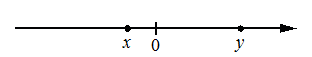
Какое из приведённых утверждений для этих чисел неверно?
1) y-x<0
2) x2y>0
3) xy<0
4) x+y>0
На каком рисунке изображено множество решений неравенства x2-17x+72≥0?
1) 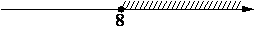
2) 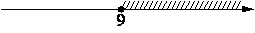
3) 
4) 
Комментарии: