Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Чтобы найти точку пересечения графиков функций, надо составить систему уравнений из этих функций и решить ее:
2x-y=-8
x+2y=6
Умножим первое уравнение на 2:
(2x-y)2=-8*2
x+2y=6
4x-2y=-16
x+2y=6
Теперь сложим уравнения, чтобы избавиться от y:
(4x-2y)+(x+2y)=-16+6
4x-2y+x+2y=-10
5x=-10
x=-2 - это и есть абсцисса точки С
Ответ: -2
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.
Расположите в порядке возрастания числа a-1, 1/a, a.
1) a, 1/a , a-1
2) a, a-1, 1/a
3) a-1, a, 1/a
4) 1/a, a-1, a
На координатной прямой отмечено число a.
Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-5)2<1
3) a2<25
4) a2>36
На координатной прямой отмечены числа а и с.
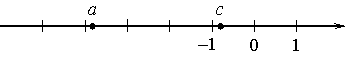
Какое из следующих утверждений неверно?
1) c-a<0
2) ac>0
3) 0<c+1<1
4) -a>0
Одно из чисел √40, √46, √53, √58 отмечено на прямой точкой A.
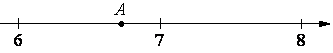
Какое это число?
1) √40
2) √46
3) √53
4) √58
На каком рисунке изображено множество решений системы неравенств
x>3,
4-x<0?
1) 
2) 
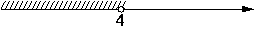
3) 
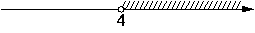
4) 
Хочу получать новые решения
Ни какого спама
Автор: Таська
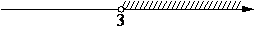
Комментарии: