
Задача №10 из 42 |
Решите уравнение x2+10x+21=0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Решим это квадратное уравнение через дискриминант:
D=102-4*1*21=100-84=16
x1=(-10+4)/(2*1)=-6/2=-3
x2=(-10-4)/(2*1)=-14/2=-7
Наименьший корень - это x2=-7.
Ответ: -7
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x2=9.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) длительность прямого авиаперелёта Москва – Гавана | 1) 14,6 секунды |
| Б) бронзовый норматив ГТО по бегу на 100 м для мальчиков 16–17 лет | 2) 60190 суток |
| В) время одного оборота Нептуна вокруг Солнца | 3) 13 часов |
| Г) длительность эпизода мультипликационного сериала | 4) 22 минуты |
Найдите корень уравнения 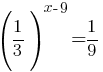
Найдите корень уравнения 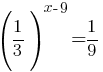
Решите уравнение x2=9.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Комментарии: