Выписаны первые несколько членов геометрической прогрессии: 1512; -252; 42; … Найдите сумму первых четырёх её членов.
В
геометрической прогрессии зависимость членов прогрессии можно записать так: bn+1=bnq
Тогда:
b2=b1q
-252=1512q
q=-252/1512=-63/378=-7/42=-1/6
b4=b3q=42*(-1/6)=-7
Тогда сумму первых четырех членов
геометрической прогрессии можно вычисли или по формуле или "в лоб":
1) "в лоб"
S4=1512+(-252)+42+(-7)=1295
2) по формуле
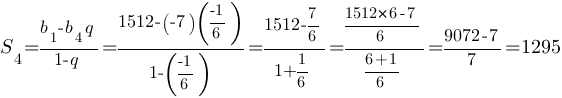
Ответ: 1295
Поделитесь решением
Присоединяйтесь к нам...
В геометрической прогрессии сумма первого и второго членов равна 50, а сумма второго и третьего членов равна 200. Найдите первые три члена этой прогрессии.
Геометрическая прогрессия задана условием bn=62,5*2n. Найдите сумму первых её 4 членов.
(bn) — геометрическая прогрессия, знаменатель прогрессии равен 1/5, b1=250. Найдите сумму первых 6 её членов.
Дана арифметическая прогрессия (an), в которой a9=-15,7, a18=-22,9.
Найдите разность прогрессии.
В геометрической прогрессии сумма первого и второго членов равна 48, а сумма второго и третьего членов равна 144. Найдите первые три члена этой прогрессии.
Хочу получать новые решения
Ни какого спама
Автор: Таська
,
Комментарии: