Выписаны первые несколько членов арифметической прогрессии: 2; 6; 10; … Найдите её шестнадцатый член.
n-ый член
арифметической прогрессии равен a1+(n-1)d
a1=2 (по условию)
a2=6 (по условию)
d=a2-a1=6-2=4
a16=a1+(n-1)d=2+(16-1)4=2+60=62
Ответ: a16=62
Поделитесь решением
Присоединяйтесь к нам...
Записаны первые три члена арифметической прогрессии: 30; 27; 24. Какое число стоит в этой арифметической прогрессии на 101-м месте?
Геометрическая прогрессия задана условием bn=-124*2n. Найдите сумму первых её 4 членов.
Геометрическая прогрессия задана условием bn=51,5(-2)n. Найдите b4.
Дана арифметическая прогрессия (an), разность которой равна -4,9, a1=-6,4. Найдите a15.
Геометрическая прогрессия задана условиями b1=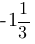
, bn+1=-3bn. Найдите b7.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: