
 Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
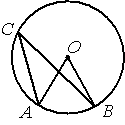
Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=70°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 70°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 70/2=35.
Ответ: /ACB=35°.
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
 Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Комментарии: