
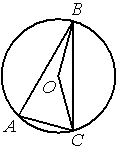
 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
По условию ∠BOC=160°, этот угол является
центральным, соответственно дуга ВC (малая часть) тоже равна 160°. ∠BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, ∠BAC=160°/2=80°.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
 На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
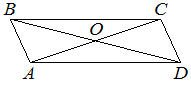 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
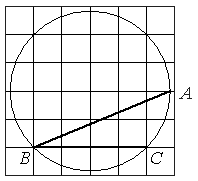 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
Комментарии:
(2017-01-11 15:06:19) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-11 15:03:57) : часы показывают 15ч какое время будут показывать чсы если минутная стрелка повернётся