
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
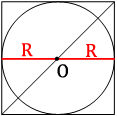 Проведем радиусы окружности, как показано на рисунке.
Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*14√
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(28√
b2=2*282*2
b2=282*22=(28*2)2=562
b=56
Ответ: 56
Поделитесь решением
Присоединяйтесь к нам...
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
 Радиус окружности, описанной около квадрата, равен 14√
Радиус окружности, описанной около квадрата, равен 14√
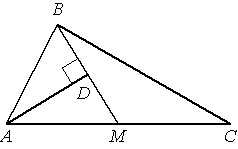 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
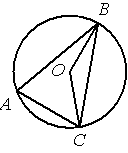 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Комментарии:
(2019-02-21 09:52:16) Администратор: Майкл, Вы правы, в решение вкралась ошибка. Спасибо большое, что заметили. Все исправлено!
(2019-02-21 00:54:00) Майкл: У вас получается , что лишь половина диагонали равно 28 , так как вы брали маленький треугольник , а просили Диагональ квадрата .Если а=14 корней из 2 ( то есть радиус , то тогда у вас диагональ меньше , чем сторона квадрата , а это невозможно.28 корней из двух больше 28