
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ524 –Є–Ј 1087 |
 –Т–µ—А—И–Є–љ—Л —А–Њ–Љ–±–∞ —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ—Л –љ–∞ —Б—В–Њ—А–Њ–љ–∞—Е –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –∞ —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–µ–є —А–Њ–Љ–±–∞ –Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є –Њ—В–љ–Њ—И–µ–љ–Є–µ –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ–Њ 31.
–Т–µ—А—И–Є–љ—Л —А–Њ–Љ–±–∞ —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ—Л –љ–∞ —Б—В–Њ—А–Њ–љ–∞—Е –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –∞ —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–µ–є —А–Њ–Љ–±–∞ –Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є –Њ—В–љ–Њ—И–µ–љ–Є–µ –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ–Њ 31.
 –Ф–ї—П —Г–і–Њ–±—Б—В–≤–∞ –≤–≤–µ–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П:
–Ф–ї—П —Г–і–Њ–±—Б—В–≤–∞ –≤–≤–µ–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П:
a - —Б—В–Њ—А–Њ–љ–∞
—А–Њ–Љ–±–∞ (–Њ–љ–Є —А–∞–≤–љ—Л –њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —А–Њ–Љ–±–∞)
d - –і–Є–∞–≥–Њ–љ–∞–ї—М AC
31d - –і–Є–∞–≥–Њ–љ–∞–ї—М BD (–њ–Њ —Г—Б–ї–Њ–≤–Є—О)
AE - k
EB - t
–Я–ї–Њ—Й–∞–і—М
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —З–µ—А–µ–Ј –і–Є–∞–≥–Њ–љ–∞–ї–Є —А–∞–≤–љ–∞ BD*AC*sinα/2 = 31d*d*sinα/2 = 15,5d2*sinα, –≥–і–µ α - —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є (–њ—А–Є —З–µ–Љ –љ–µ –≤–∞–ґ–љ–Њ –Ї–∞–Ї–Њ–є, —В–∞–Ї –Ї–∞–Ї —Б–Є–љ—Г—Б—Л –Њ–±–Њ–Є—Е —Г–≥–ї–Њ–≤ –±—Г–і—Г—В —А–∞–≤–љ—Л –і—А—Г–≥ –і—А—Г–≥—Г).
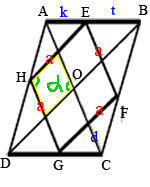 –Ґ–∞–Ї –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л
—А–Њ–Љ–±–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ, –Њ–±—А–∞–Ј—Г–µ—В—Б—П –Љ–∞–ї–µ–љ—М–Ї–Є–є
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ, –∞ –Ј–љ–∞—З–Є—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–µ —Г–≥–ї—Л —А–∞–≤–љ—Л (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞).
–Ґ–∞–Ї –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л
—А–Њ–Љ–±–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ, –Њ–±—А–∞–Ј—Г–µ—В—Б—П –Љ–∞–ї–µ–љ—М–Ї–Є–є
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ, –∞ –Ј–љ–∞—З–Є—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–µ —Г–≥–ї—Л —А–∞–≤–љ—Л (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC –Є EBF.
∠EBF - –Њ–±—Й–Є–є
∠BFE=∠BCA (—Н—В–Њ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ—Л–µ —Г–≥–ї—Л)
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC –Є EBF
–њ–Њ–і–Њ–±–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П).
–Ґ–Њ–≥–і–∞ EF/AC=a/d=t/(t+k)
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ,
–њ–Њ–і–Њ–±–љ—Л –Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABD –Є AEH.
–Ф–ї—П –љ–Є—Е —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ: a/31d=k/(t+k)
–°–Ї–ї–∞–і—Л–≤–∞–µ–Љ —Н—В–Є –і–≤–∞ —Г—А–∞–≤–љ–µ–љ–Є—П:
a/d+a/31d=t/(t+k)+k/(t+k)
31a/31d+a/31d=(t+k)/(t+k)
32a/31d=1
32a=31d
a=31d/32
S—А–Њ–Љ–±–∞=a2sinα
S–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞=15,5d2*sinα (—Н—В–Њ –Љ—Л –≤—Л—П—Б–љ–Є–ї–Є —А–∞–љ–µ–µ)
S—А–Њ–Љ–±–∞/S–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞=(a2sinα)/(15,5d2*sinα)=a2/(15,5d2)=(31d/32)2/(15,5d2)=(312*d2)/(322*15,5*d2)=961/(1024*15,5)=62/1024=31/512
–Ю—В–≤–µ—В: 31/512
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
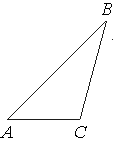 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї A —А–∞–≤–µ–љ 45¬∞, —Г–≥–Њ–ї B —А–∞–≤–µ–љ 30¬∞, BC=6√
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї A —А–∞–≤–µ–љ 45¬∞, —Г–≥–Њ–ї B —А–∞–≤–µ–љ 30¬∞, BC=6√
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2√
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠BAC=62¬∞, AD вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BAD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ ∠BAC=62¬∞, AD вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BAD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 28, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 28, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–Ъ–∞–Ї–Є–µ –Є–Ј –і–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –Х—Б–ї–Є –њ—А–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є–Є –і–≤—Г—Е –њ—А—П–Љ—Л—Е —В—А–µ—В—М–µ–є –њ—А—П–Љ–Њ–є –≤–љ—Г—В—А–µ–љ–љ–Є–µ –љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л —А–∞–≤–љ—Л 90¬∞, —В–Њ —Н—В–Є –і–≤–µ –њ—А—П–Љ—Л–µ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л.
2) –Т –ї—О–±–Њ–є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М.
3) –¶–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —П–≤–ї—П–µ—В—Б—П —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б–µ—А–µ–і–Є–љ–љ—Л—Е –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–Њ–≤ –Ї —Б—В–Њ—А–Њ–љ–∞–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: