
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
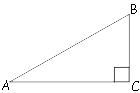 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√
BC=AC√
S=AC*(AC√
AC2/2=2
AC2=4
AC=2
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
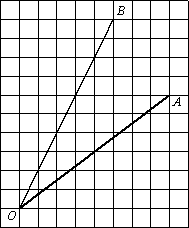 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
 Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Комментарии: