
 Радиус окружности, описанной около квадрата, равен 14√
Радиус окружности, описанной около квадрата, равен 14√
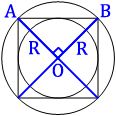 Проведем диаметры
описанной окружности, как показано на первом рисунке.
Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(14√
AB2=2*142*2
AB2=142*22=(14*2)2=282
AB=28
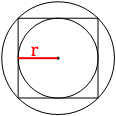 Проведем радиус
вписанной окружности, как на втором рисунке.
Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=28/2=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
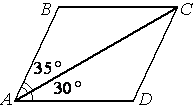 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
 Катеты прямоугольного треугольника равны 3√
Катеты прямоугольного треугольника равны 3√
Комментарии: