
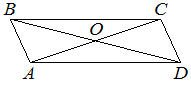
 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
По
третьему свойству параллелограмма:
DO=BD/2=20/2=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
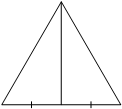 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
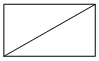 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Комментарии:
(2023-05-16 11:36:07) : Диогонали AC и BD параллелограмма ABCD пересекаются в точке O AC=20 BD=26 AB= 8 Найдите DO