
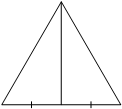
 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
 Введем обозначения как показано на рисунке.
Введем обозначения как показано на рисунке.
По
определению равностороннего треугольника:
AB=BC=AC=14√3
По
свойству равностороннего треугольника, медиана является так же и
биссектрисой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2 (т.к. AC - медиана).
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
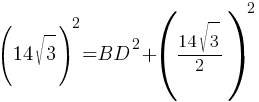
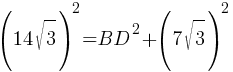
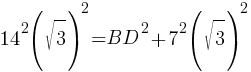
196*3=BD2+49*3
588=BD2+147
BD2=588-147=441
BD=√441=21
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
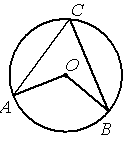 Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
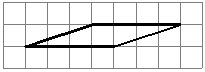 На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
Комментарии: