
 Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
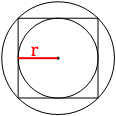 Проведем радиус
вписанной окружности, как на рисунке.
Проведем радиус
вписанной окружности, как на рисунке.
Очевидно, что r=a/2, где а - сторона
квадрата.
a=2r=2*2√2=4√2
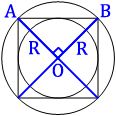 Проведем диаметры
описанной окружности, как показано на втором рисунке.
Проведем диаметры
описанной окружности, как показано на втором рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=OA2+OB2
a2=R2+R2
a2=2R2
(4√2)2=2R2
16*2=2R2
16=R2
R=√16=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
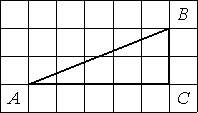 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
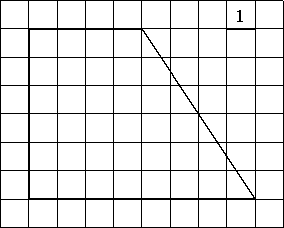 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
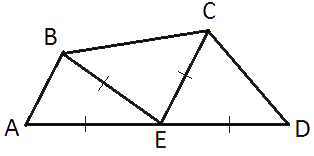 Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
Комментарии: