Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE, эти треугольники
подобны, т.к. ∠C - общий, ∠B и ∠DEC - прямые, а углы A и EDC - равны, так как являются
соответственними.
Из подобия этих треугольников следует, что AB/DE=BC/EC, отсюда AB=(BC*DE)/EC=((17+8)*1,6)/8=5 м.
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
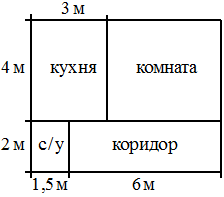Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3м x 4м, санузел — 1,5м x 2м, длина коридора 6м. Найдите площадь комнаты (в квадратных метрах).
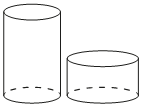Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
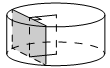Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
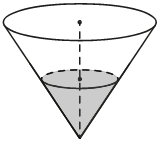В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
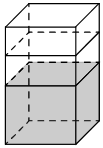В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре
1000 кубических сантиметров.
Хочу получать новые решения
Ни какого спама
Автор: Таська
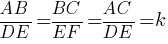
Комментарии: