
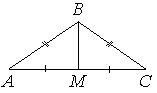
 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
Треугольник ABC -
равнобедренный (по условию).
Тогда, по третьему свойству равнобедренного треугольника, BM является высотой.
Т.е. треугольник ABM - прямоугольный.
AM=AC/2=24/2=12 (так как BM -
медиана).
По теореме Пифагора:
AB2=BM2+AM2
152=BM2+122
225=BM2+144
BM2=81
BM=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
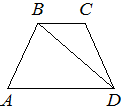 В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
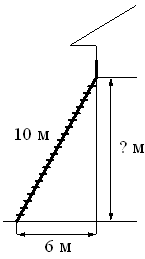 Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
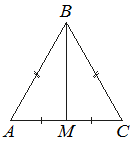 В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
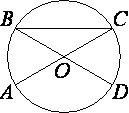 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.

Комментарии: