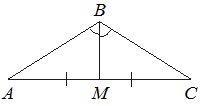
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
Так как медиана делит угол пополам, то она так же является и
биссектрисой. Одновременно быть и
биссектрисой и медианой отрезок может только в равнобедренном треугольнике (по
свойству равнобедренного треугольника), тогда этот отрезок так же является и
высотой.
Т.е. треугольник ABM - прямоугольный.
∠ABM=∠B/2=120°/2=60°
Так как ABM прямоугольный, то по определению косинуса:
cos∠ABM=BM/AB
cos60°=27/AB (cos60°=1/2 по таблице)
1/2=27/AB |*2
1=54/AB
AB=54
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
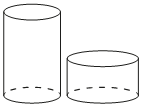Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
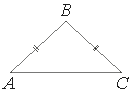В равнобедренном треугольнике ABC основание AC равно 40, площадь треугольника равна 300. Найдите длину боковой стороны AB.
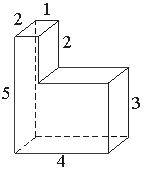Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
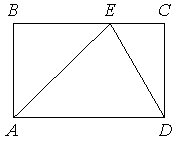На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: