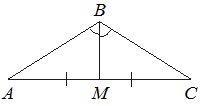
В треугольнике ABC угол B равен 120°. Медиана BM делит угол B пополам и равна 27. Найдите длину стороны AB.
Так как медиана делит угол пополам, то она так же является и
биссектрисой. Одновременно быть и
биссектрисой и медианой отрезок может только в равнобедренном треугольнике (по
свойству равнобедренного треугольника), тогда этот отрезок так же является и
высотой.
Т.е. треугольник ABM - прямоугольный.
∠ABM=∠B/2=120°/2=60°
Так как ABM прямоугольный, то по определению косинуса:
cos∠ABM=BM/AB
cos60°=27/AB (cos60°=1/2 по таблице)
1/2=27/AB |*2
1=54/AB
AB=54
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
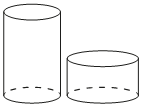Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
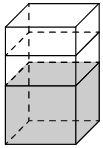В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
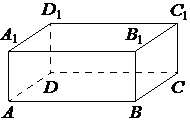В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: