
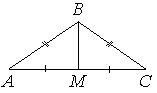
 В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM.
Треугольник ABC -
равнобедренный (по условию).
Тогда, по третьему свойству равнобедренного треугольника, BM является высотой.
Т.е. треугольник ABM - прямоугольный.
AM=AC/2=24/2=12 (так как BM -
медиана).
По теореме Пифагора:
AB2=BM2+AM2
152=BM2+122
225=BM2+144
BM2=81
BM=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
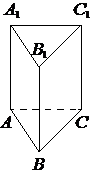 Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
 Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
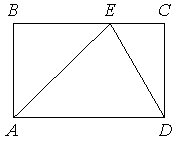 На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.
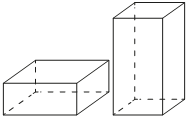 Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре с половиной раза ниже второй,
а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
 Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.



Комментарии: