
 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
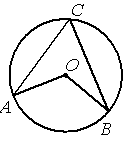
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=65°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 65°*2=130°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=130°.
Ответ: /AOB=130°.
Поделитесь решением
Присоединяйтесь к нам...
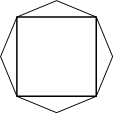 Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
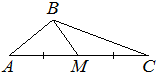 В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Комментарии: