Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции, а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине гипотенузы (
по свойству прямоугольного треугольника), h=3/2=1,5. Используя формулу площади трапеции получаем S=(2+6)*1,5/2. Вычисляем S=6.
Ответ: S=6.
Поделитесь решением
Присоединяйтесь к нам...
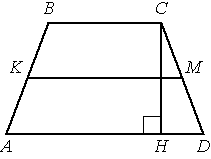В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
Найдите площадь треугольника, изображённого на рисунке.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Площадь прямоугольного треугольника равна 882√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-02-06 21:50:52) Дарья: Спасибо огромное автору и сайту за проделанную работу.Это очень помогает и выручает в той ситуации,когда не можешь решить то или иное задание.Спасибо!