
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k>0, b<0 Б) k>0, b>0 В) k<0, b>0 |
1)  |
2)  |
3)  |
Если прямая слева направо возрастает, то k>0 (как на графиках 1) и 2)), и наоборот, если прямая слева направо убывает, то k<0 (как на графике 3).
Узнать знак коэффициента b, можно приравняв х к нулю. Получим: y=k*0+b=b.
Посмотрим на график и узнаем b больше нуля или меньше. Т.е коэффициент b - это координата "y" точки пересечения прямой и оси y. Тогда:
Для графика 1): k>0, b>0 - вариант Б)
Для графика 2): k>0, b<0 - вариант A)
Для графика 3): k<0, b>0 - вариант В)
Ответ: 1) - Б), 2) - А), 3) - В)
Поделитесь решением
Присоединяйтесь к нам...
При каких отрицательных значениях k прямая y=kx-4 имеет с параболой y=x2+3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Одна из точек, отмеченных на координатной прямой, соответствует числу 8/9. Какая это точка?

1) А
2) B
3) C
4) D
Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?

1) 10/23
2) 12/23
3) 13/23
4) 14/23
На каком рисунке изображено множество решений системы неравенств
 x>-1,
x>-1,
3-x>0?
1) 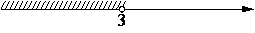
2) 
3) система не имеет решений
4) 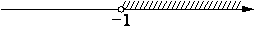
Постройте график функции 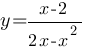 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Комментарии: