Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
Рассмотрим каждое утверждение.
1) "Каждая из биссектрис равнобедренного треугольника является его высотой", это утверждение неверно, т.к. по
свойству равнобедренного треугольника, только биссектриса, проведенная к основанию является его высотой.
2) "Диагонали прямоугольника равны", это утверждение верно (по
свойству прямоугольника).
3) "У любой трапеции основания параллельны", это утверждение верно (по
определению трапеции).
Поделитесь решением
Присоединяйтесь к нам...
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
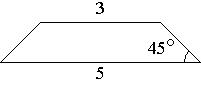В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-11-04 15:37:54) Ксения: Сторона ромба равна 7, а один из углов равен 150°. Найдите высоту