На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Для вычисления площади треугольника существует несколько формул. Ни для одной из них у нас не хватает данных.
Значит недостающие данные надо получить.
Посмотрим, что общее есть у треугольников ABC и BCD:
1. Сторона BC
2. Угол BCD.
Тогда лучше воспользоваться
формулой "через две стороны и угол между ними".
Площадь треугольника ABC:
SABC=(1/2)*AC*BC*sin∠BCD
SABC=(1/2)*(AD+DC)*BC*sin∠BCD
20=(1/2)*(3+7)*BC*sin∠BCD
20=(1/2)*10*BC*sin∠BCD
20=5*BC*sin∠BCD
BC*sin∠BCD=4
Площадь треугольника BCD:
SBCD=(1/2)*DC*BC*sin∠BCD
Подставляем значение BC*sin∠BCD, полученное ранее, и значение DC, известное из условия:
SBCD=(1/2)*7*4
SBCD=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
Медиана равностороннего треугольника равна 9√
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
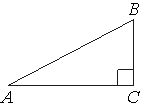В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
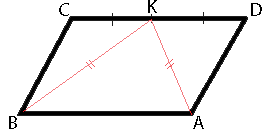В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
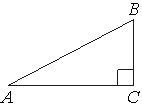В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: