
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. ON=AO/2
При этом AN=AO+ON
27=AO+ON, подставляем в это уравнение первое равенство:
27=AO+AO/2 |*2
54=2AO+AO
54=3AO
AO=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
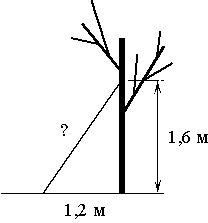 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
 Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
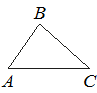 В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Комментарии: