Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
По третьему свойству вписанной окружности, радиус вписанной окружности равен:
r=S/p, где S - площадь треугольника, а p - полупериметр.
p=48/2=24
S=r*p=3*24=72
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
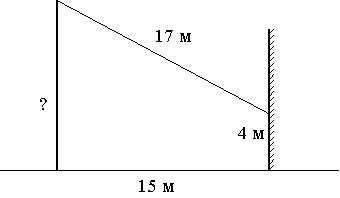От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-04-26 20:11:27) галина: есть ли другое решение задачи 936 из1087 для чего дается сторона
(2023-04-26 20:03:19) галина: все свойства вписанной окружности