
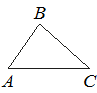
 В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
По
теореме косинусов:
AC2=AB2+BC2-2*AC*BC*cos∠ABC
122=82+102-2*8*10*cos∠ABC
144=64+100-160*cos∠ABC
144=164-160*cos∠ABC
-20=-160*cos∠ABC |:(-20)
1=8cos∠ABC
cos∠ABC=1/8=0,125
Ответ: 0,125
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
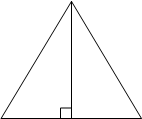 Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√
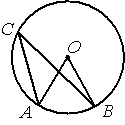 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Комментарии:
(2020-03-09 21:23:08) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-02-25 11:05:38) : Ав=вс Ав=15,2 BN=7,6 НАЙТИ углы авс
(2017-11-13 21:38:05) Администратор: Mauzsz, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-11-11 05:23:37) Mauzsz: в треугольнике ABC дано: AB=11, AC=9, cosA=83/99 Найти: сторону BC