
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ697 –ł–∑ 1087 |
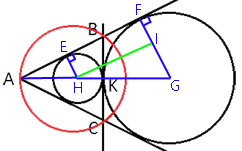
 –Ē–≤–Ķ –ļ–į—Ā–į—é—Č–ł–Ķ—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ K –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ä–į–ī–ł—É—Ā—č –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–≤–Ĺ—č 31 –ł 32, –ļ–į—Ā–į—é—ā—Ā—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ —É–≥–Ľ–į —Ā –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ A. –ě–Ī—Č–į—Ź –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź –ļ —ć—ā–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ź–ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É K, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —É–≥–Ľ–į –≤ —ā–ĺ—á–ļ–į—Ö B –ł C. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.
–Ē–≤–Ķ –ļ–į—Ā–į—é—Č–ł–Ķ—Ā—Ź –≤–Ĺ–Ķ—ą–Ĺ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ K –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ä–į–ī–ł—É—Ā—č –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–≤–Ĺ—č 31 –ł 32, –ļ–į—Ā–į—é—ā—Ā—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ —É–≥–Ľ–į —Ā –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ A. –ě–Ī—Č–į—Ź –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź –ļ —ć—ā–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ź–ľ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É K, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —É–≥–Ľ–į –≤ —ā–ĺ—á–ļ–į—Ö B –ł C. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.
 –ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤:
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤:
EH - —Ä–į–ī–ł—É—Ā –ľ–į–Ľ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ě–Ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ķ–Ĺ AB (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ).
FG - —Ä–į–ī–ł—É—Ā –Ī–ĺ–Ľ—Ć—ą–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ě–Ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ķ–Ĺ AB (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ).
HG - –ĺ—ā—Ä–Ķ–∑–ĺ–ļ, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–ł–Ļ —Ü–Ķ–Ĺ—ā—Ä—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ł —Ä–į–≤–Ĺ—č–Ļ R+r, —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É –ö.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AFG –ł AEH:
∠EAH - –ĺ–Ī—Č–ł–Ļ;
—É–≥–Ľ—č AEH –ł AFG - –Ņ—Ä—Ź–ľ—č–Ķ.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ —ć—ā–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č, —ā–ĺ–≥–ī–į:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
32/31=(AH+R+r)/AH
32AH=31(AH+63)
32AH-31AH=1953
AH=1953
sin∠EAH=EH/AH=31/1953=1/63
AK=AH+r=1953+31=1984
AK –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ķ–Ĺ BC, —ā.–ļ. —ć—ā–ĺ –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ī–ĺ–Ľ—Ć—ą–ĺ–≥–ĺ –ł –ľ–į–Ľ–ĺ–≥–ĺ —Ä–į–ī–ł—É—Ā–ĺ–≤, –į AB -
–ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź (
—Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ). AK –ī–Ķ–Ľ–ł—ā —Ö–ĺ—Ä–ī—É AB –Ņ–ĺ–Ņ–ĺ–Ľ–į–ľ (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ö–ĺ—Ä–ī—č).
–Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC -
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ, —ā.–ļ. AK - –ł
–ľ–Ķ–ī–ł–į–Ĺ–į –ł
–≤—č—Ā–ĺ—ā–į (
—Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
–Ę–Ķ–Ņ–Ķ—Ä—Ć —É–Ī–Ķ—Ä–Ķ–ľ –ł–∑ —Ä–ł—Ā—É–Ĺ–ļ–į –≤—Ā–Ķ, —á—ā–ĺ –Ĺ–į—Ā –Ī–ĺ–Ľ—Ć—ą–Ķ –Ĺ–Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā—É–Ķ—ā –ł —Ä–Ķ–∑—é–ľ–ł—Ä—É–Ķ–ľ, —á—ā–ĺ –ľ—č –∑–Ĺ–į–Ķ–ľ:
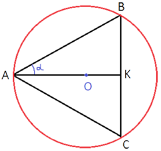 AK=1984
AK=1984
sinα=1/63
–Ę–į–ļ –ļ–į–ļ AK -
–Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į, —ā–ĺ —Ü–Ķ–Ĺ—ā—Ä –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į AK.
–Ě–į–Ļ–ī–Ķ–ľ AB.
–ü–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ü–ł—Ą–į–≥–ĺ—Ä–į:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=
19842
AB2(1-1/632)=19842
AB2(632-1)=632*19842
AB2=632*19842/(632-1)
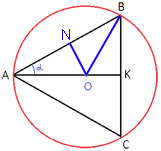 –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ AOB.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ AOB.
AO=OB, —ā–į–ļ –ļ–į–ļ —ć—ā–ĺ —Ä–į–ī–ł—É—Ā—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–į–Ĺ–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –≤—č—Ā–ĺ—ā—É ON, –≤
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –ĺ–Ĺ–į —ā–į–ļ –∂–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł
–ľ–Ķ–ī–ł–į–Ĺ–ĺ–Ļ (–Ņ–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į).
sinα=ON/AO => ON=AO/63
–ü–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ
–ü–ł—Ą–į–≥–ĺ—Ä–į:
AO2=ON2+AN2
AO2=AO2/632+(AB/2)2
AO2-AO2/632=AB2/4
AO2(1-1/632)=AB2/4
AO2((632-1)/632)=(632*19842/(632-1))/4
4AO2=632*19842/(632-1)/((632-1)/632)=632*19842*632/(632-1)2
2AO=632*1984/(632-1)
2AO=3969*1984/3968=3969/2=1984,5
AO=992,25
–ě—ā–≤–Ķ—ā: 992,25
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ PK, –Ķ—Ā–Ľ–ł BH=13.
–Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ PK, –Ķ—Ā–Ľ–ł BH=13.
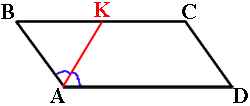 –Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=6, CK=10.
–Ď–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į —É–≥–Ľ–į A –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É BC
–≤ —ā–ĺ—á–ļ–Ķ K. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į, –Ķ—Ā–Ľ–ł BK=6, CK=10.
 –Ě–į–Ļ–ī–ł—ā–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć –ź–° –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ –ź–í —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 30¬į –ł 45¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć –ź–° –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ –ź–í —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 30¬į –ł 45¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
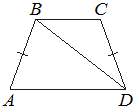 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AB=CD, ∠BDA=38¬į –ł ∠BDC=32¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AB=CD, ∠BDA=38¬į –ł ∠BDC=32¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –†–į–ī–ł—É—Ā –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ –ļ–≤–į–ī—Ä–į—ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7√
–†–į–ī–ł—É—Ā –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ –ļ–≤–į–ī—Ä–į—ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7√
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2017-03-21 19:51:48) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ú–į—Ä–ł—Ź, –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ —ć—ā–ĺ –ĺ–Ņ–Ķ—á–į—ā–ļ–į, —Ā–Ņ–į—Ā–ł–Ī–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ, —á—ā–ĺ –∑–į–ľ–Ķ—ā–ł–Ľ–ł. –ė—Ā–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ĺ.
(2017-03-19 18:42:33) –ú–į—Ä–ł—Ź: –ź–ö –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ķ–Ĺ –ź–í!!! –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –í–°?